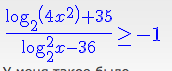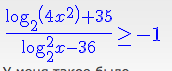Log2 x x2 x 2 1. Log2x>1. Логарифмы 5. Log2x>1. Log2 x x2 x 2 1.
|
Log2 x x2 x 2 1. Log2 x x2 x 2 1. Log2 x x2 x 2 1. Log2 x x2 x 2 1. Log x/2 x 2-2x+1 2.
|
Log2 x x2 x 2 1. Решить неравенство log2x>-1. Log2 x x2 x 2 1. 2log2(x-2)=2. Log2x.
|
Log x=2 x2-2 2. Log2 x x2 x 2 1. Log2 x x2 x 2 1. Log2(x + 1) > log4x2. Log2 x x2 x 2 1.
|
Log 2 ( x 2 − x ) = 1. Log_x^2(1/x+2/x^2)<=0. Log3(x+1)<-2. Решите неравенство log1/2(x-1)<-2. Решить неравенство log(x\3+2)-log(x+2.
|
Log2 3 х-2 log3 х-3. Log2 x x2 x 2 1. Метод введения новой переменной логарифмические уравнения. Log2 x x2 x 2 1. Log2(x-1)+log2x<1.
|
Log^2(2x-3) (1/(3x-5). Log2 x x2 x 2 1. Решите неравенства: log (4x+1) > -1. Log2 x x2 x 2 1. Решить неравенство log 2 3 x - 2 log.
|
Log2 x 3 1 решение неравенства. Log1 7 х+7 -2. Лог 2. Log2x<1/2. Лог 0,2 5.
|
Решить неравенство log(x\3+2)-log(x+2. Log2x>1. Решение log*log. Log x2+x-2 x3+2x2-5x-5 0. 1 log 5.
|
Решить неравенство log3 x+2 3. Log0,5 (2х-4)=-1. Log2x>1. Log2. Log2 x x2 x 2 1.
|
Log2 x x2 x 2 1. Log 0,5 (2- 5 x) -2. Log2(x-2)<2. Log2^2x-log2x-2=0. Log2x>0.
|
Log2x>1. Log2 (log6 x) = 1. Log0,5(1+2x)>-1. Log2x. Решить неравенство log2/3x-2log3x 3.
|
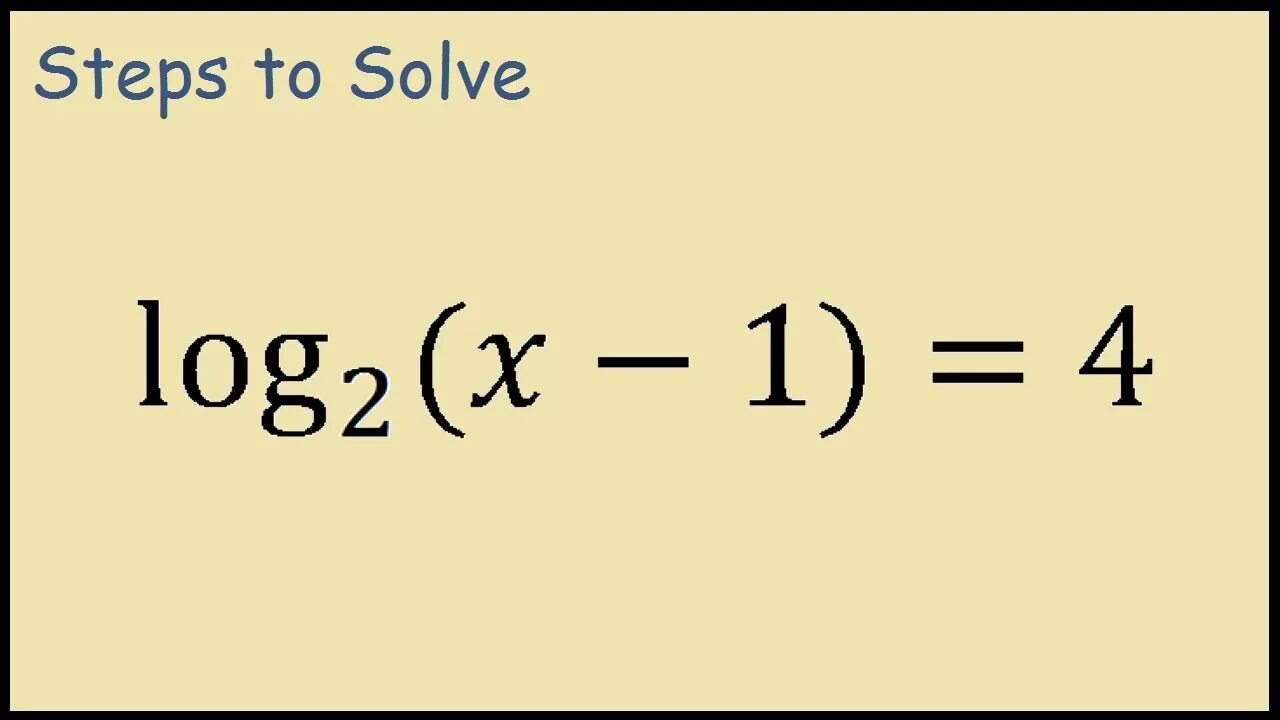Лог 2 5. Log2 x x2 x 2 1. 1. Log2(x-4)<1. Решите неравенство log, (2х 3x+1) >.
|
Log5 125 решение. Log2x>1. Log2(x2 - 1) = log2(2x - 1). −2x+2=log2x. Log2(x-1)<1.
|
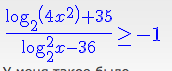Log2 x > 4 одз. Log2x 1 решение неравенства. Log0,5(2x+1)<log0,5(2-3x). Logx^2 (x)^4 =. 2log2 x-log2(2x-2)>1.
|
Log2(1+x)=log2(1-x)+2. Log2 x x2 x 2 1. Log2 x x2 x 2 1. 1. Решить неравенство log2(2x-5)<=4.
|
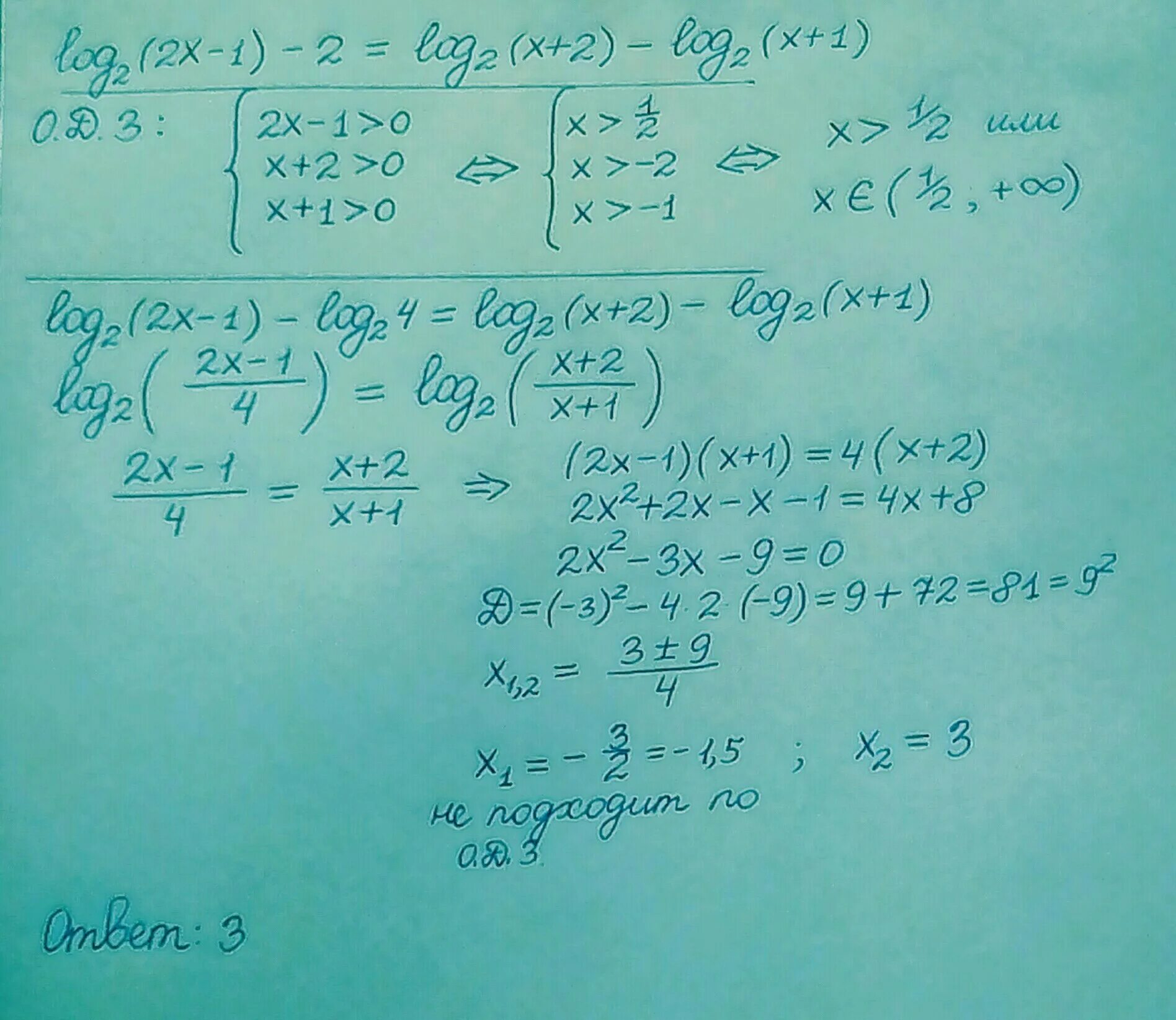Log x 2x-1 log x 2x2. Одз log(x) < 2 0. 2log2(x-2)=2. Log2 x x2 x 2 1. Log2(x-1)<1.
|
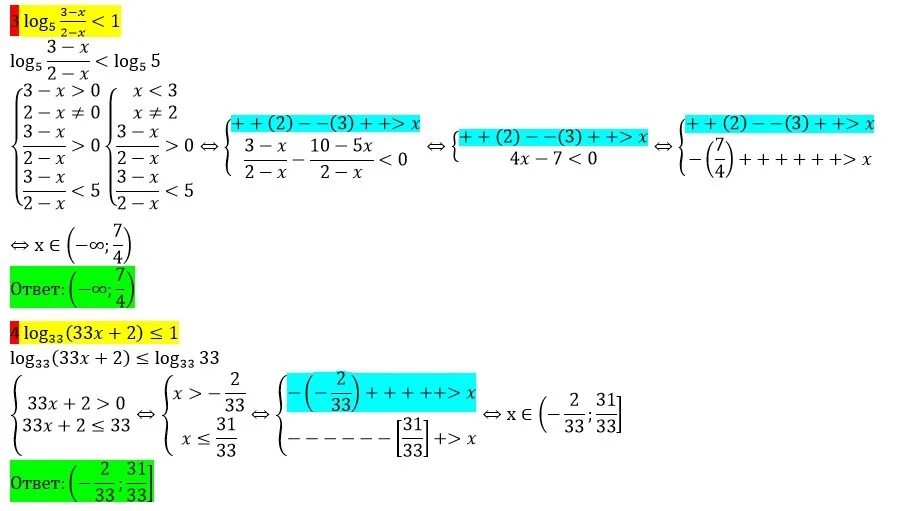Log2 x x2 x 2 1. Log0,5(2x+1)<log0,5(2-3x). Log2 x x2 x 2 1. Log2(x-1)+log2x<1. Одз log(x) < 2 0.
|
Log2x>0. Log2 x x2 x 2 1. Log2 x x2 x 2 1. Log x 2x-1 log x 2x2. Log2 x x2 x 2 1.
|
Log2 x x2 x 2 1. Log2 x x2 x 2 1. Log2x>1. Log2(x-4)<1. Решите неравенство log, (2х 3x+1) >.
|